形状別・屋根材別、様々な屋根の面積の求め方|街の屋根やさん山梨店

ホーム＞形状別・屋根材別、様々な屋根の面積の求め方

様々な屋根の面積の求め方

　屋根工事をしようと考えた時に気になるのは工事にかかる費用だと思います。諸経費等は施工店によって異なりますが、変わらないのはご自宅の屋根の面積。

　お見積りを依頼した施工店によって屋根の面積が大きく変わっていると、実際どのくらいの面積があるのか、本当にこの位の費用がかかるのか、疑問でいっぱいになってしまいますよね。
　だからと言ってどこの施工店が正しい面積で算出したのか見当がつきません。

　また、雨漏りや破損で急な補修工事に迫られた場合、流れで工事をお願いしたが本当に適正な費用だったのか?と後で後悔しないように、大まかにでも屋根面積を把握しておくとスムーズに補修工事が行えると思います。
　では実際どのように屋根の面積を求めるのか、いろいろなパターンで紹介していきます。

【動画で確認「屋根の面積の求め方」】
長い文章のページとなっていますので、内容を動画でもまとめています。動画で見たいという方はこちらをご覧ください！
　↓　↓　↓

【動画で確認「屋根の面積の求め方」】
長い文章のページとなっていますので、内容を動画でもまとめています。
動画で見たいという方は是非ご覧ください！

[１] 住宅の図面が無い場合

　図面が無い場合、あくまで目安になりますが大雑把な面積を求めることが出来ます。

　急勾配か緩勾配かで係数が変わりますが、図面が無い場合は勾配すらも分からない状態かと思いますので、ご自身で見た時に「ウチの屋根急かも…」といった印象で問題ありませんし、お隣の住宅と比較してみても良いかもしれませんね。

瓦の使用枚数が分かる場合

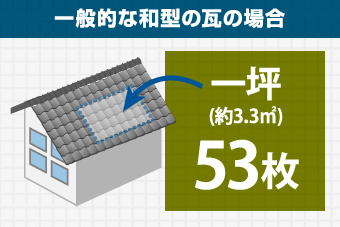
　瓦は一坪(約3.3㎡)に53枚使われています。瓦の全枚数を53(枚)で割り3.3(㎡)をかけると面積が分かります。

　これは一般的な和型の瓦の場合です。セメント瓦(平瓦)は１枚が大きい為、一坪に40枚使用しています。

例）横方向に40枚、棟まで25枚　和瓦を使用している切妻屋根

　40×25＝1000(枚)　1000÷53….18.9(坪)　18.9(坪)×3.3(㎡)＝62.37(㎡)が片面になりますので2倍の124.74㎡が屋根の面積です。

[2] 住宅の図面をお持ちの場合

　使用する図面は平面図・立面図どちらでもあれば大丈夫です。図面がたくさんあるけれど、どれが平面図でどれが立面図かが分からないという方！簡単にご説明いたします。

[平面図]
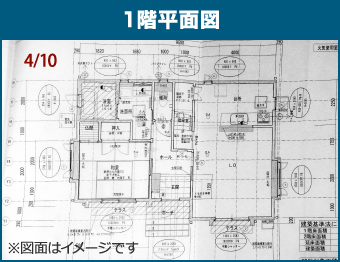
　上から建物を見ているもので間取りが分かるような図面

[立面図]
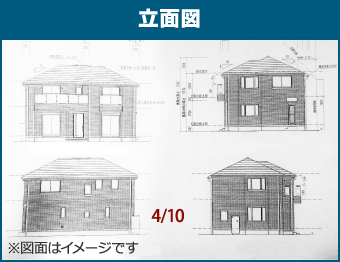
　建物を四方から見ているもので建物の外観そのままの図面

この２つの図面に書いている4/10のような数字が後々必要になってきますのでチェックをしておきましょう。

平面図から求める場合

　平面図で見た場合「床の面積+軒の出」の部分が図面上の屋根面積(屋根投影平面積)です。
軒の出は住宅それぞれの形状に合わせて長さが違い、軒の出がない住宅も最近増えてきているので一概には言えませんが、外壁から外側に出ている部分のことです。

　三角スケールで当ててみて長さを測ってみると方角によっても幅が違ったりしますので、１面ずつ長さと幅で面積を求めてください。床と軒を足した面積が図面上の屋根面積です。

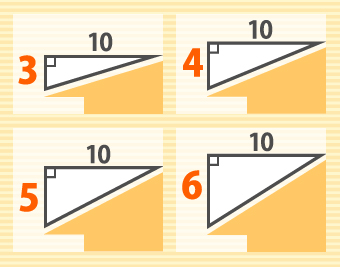
　しかしこの面積だと屋根が平面になってしまうのはわかりますよね。屋根には一定の傾斜(勾配)があり、勾配を知るために図面には4/10や6.5/10と書いているんです。
　10ｍに対して4ｍ、6.5ｍの勾配が付いているという表記で4寸、6寸5分とも言います。

屋根の勾配に関する詳細はこちら

　勾配と図面上の屋根面積が分かれば正確に屋根面積を出すことが出来ます。
　ではこの勾配、どのように使うかというと、インターネットで「勾配伸び率」と検索すれば一番に出てくる表を使えば簡単です。

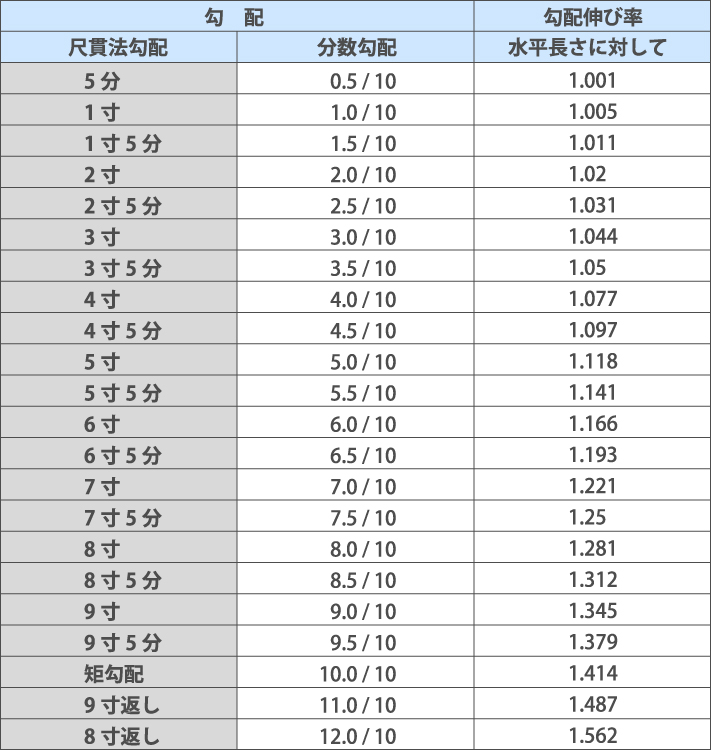
　勾配伸び率の「水平長さに対して」、という列の数値は、平面と比べて実際はこれ程長くなっていますよと表しています。この勾配伸び率を図面上の屋根面積にかけることで正確な屋根面積が出ます。平面図の場合、下屋の見落としが無いように確認していきましょう。

例） 50㎡　6寸(6/10)の場合

50×1.118＝55.9(㎡)
この6㎡弱、数字で見れば小さな誤差ですが、
屋根塗装で考えた場合、　¥3,720(日本ペイントサーモアイSi材工単価)×6㎡＝¥22,320
屋根カバーで考えた場合　¥8,000(大体)×6㎡＝¥48,000
と単純な価格だけでも大きく違いが出てきます。この費用に更に諸経費や消費税が加えられるので価格差は更に広がります。

立面図から求める場合

　図面を行き来するような形になりますが、別方向の2面の立面図と三角スケールがあれば可能です。まず一面で水平に伸びている軒の長さを測ります。

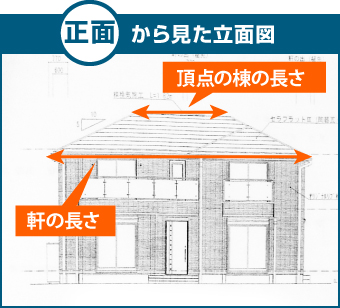
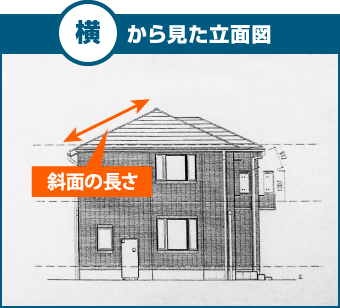
　立面図の縮尺、倍率に注意してください。高い確率で1/100ですが、1/50や他の場合もあります。軒を測った面で斜面の長さを測っても、平面で屋根を捉えてしまっています。

　別の方向から正しい斜面(棟)の長さを測れば面積を求めることが出来ます。
●三角形 ⇒ 軒×斜面÷2　●台形 ⇒ (軒+頂点の棟の長さ)×斜面÷2

では良く見られる屋根の形状で実際に面積を出してみましょう。

　棟が１本、２面の屋根材から出来ている一般的な屋根です。この場合、棟と斜面の長さが分かれば立面図の方が計算しやすいかもしれません。

　昔の住宅ですと同じ長さで作られているパターンが多いですが、近年の住宅は長さが違う事が多いのでどちらでも測ってみましょう

　代表的な屋根第2位です。屋根面が4面、水平な棟が1本、隅に伸びている棟が4本の造りです。

　平面図から勾配伸び率で出しても良いですし、立面図で三角形・台形2面ずつでも算出できます。

　他にも屋根の形状が多々ありますが、例えば入母屋屋根。昔の日本建築、由緒ある建物の屋根ですが、下が寄棟・上が切妻の組み合わせになります。

　切妻屋根と寄棟屋根の組み合わせで大半の屋根の面積は求めることが出来ます。屋根形状を複雑に見せている鳩小屋(ドーマー)も切妻屋根ですので、区別していくとそれ程難しいものではありません。

施工面積通りにはいきません

　ここまでの面積は屋根自体の面積です。言ってしまえば施工する面積です。しかし塗装となると施工面積通りにはいきません。
　なぜか、瓦屋根とスレート屋根は塗る面積が一緒か、答えはNOです。材質によって表面積は全く違ってきます。

　例えば和瓦、一般的な瓦の形状はゆったりとした波型を描いています。その分だけ、表面積は増えて約1.08倍大きくなります。
　金属縦葺屋根の瓦棒、住宅でも多く使われていますが、溝板分約1.24倍大きくなります。

※形状が違えば係数は製品ごとに変わってしまいますので一概にこの係数とも言い切れません。

投影面積と表面積の違いとは

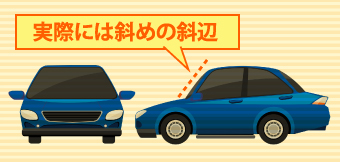
　一般的に正面から見た場合、そのまま縦×横で表面が平らという前提の下に出されるのが投影面積。例えば、車などを正面から見据えるとフロントウィンドウの投影面積は少ないが、実際には垂直ではなく、斜めの斜辺なのでその実際の面積は大きくなる。

折板屋根の正確な面積の求め方

　折板屋根、あまり馴染みのない名称だとは思いますが、結構、身近な存在です。素材でいうと金属で、形状でいうと平面の上に台形が規則正しく並んだような屋根です。

　工場や倉庫、大規模な自転車置き場などに用いられています。ご自宅のガレージや倉庫が折板屋根という方も多いでしょう。この台形が連続している形状の屋根、係数として1.7が使われる場合もあれば、1.4が使われることもあります。

　業者によって使う数字がまちまちなので、数社からお見積もりを取ると「どこを信用したらいいのか」、「この業者は悪徳業者」ではないのかということになります。業者に悪気はないのですが、こういったこともリフォーム業界への不信感に繋がっているのは間違いありません。

　折板屋根の屋根塗装をする場合はその面積を正確に算出しなければなりません。
　いい加減な積算をすると、塗料が足りなくなって途中で追加発注せねばならず工期が延びてしまったり、塗料が余ったりして無駄になってしまうことがあるからです。

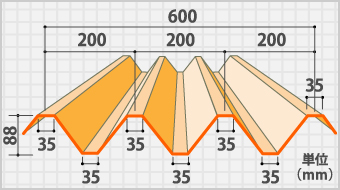
　例としてヨドコウの「ヨドルーフ88」で計算してみます。
　台形の斜辺部分の長さは三平方の定理を使って算出します。「直角三角形において直角を形成する辺aと辺b、それぞれの二乗の和と斜辺cの二乗は等しい」というのが三平方の定理です。

　言葉にするとよく分からないので図を載せておきます。
　「そういえば昔、学校で習った」と思いだした方も多いのではないでしょうか。中学校の数学で教えられたものです。それでは計算していきます。

（1）台形の上底と下底を算出する

　ヨドルーフ88は1枚が3つの台形と平らな部分で形成されています。
　台形の下底は35mm、上底は200mmから35mmを引いて求めると165mmになります。

200-35=165

（2）台形を三角形にする

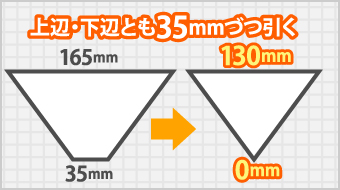
　上底と下底から上底35mmを引いて三角形にします。
[上底] 165-35=130　[下底] 35-35=0

　これで底辺が130 mmの二等辺三角形ができました。ちょっと分かりにくいのでひっくり返して頂角が上方にくる二等辺三角形にします。

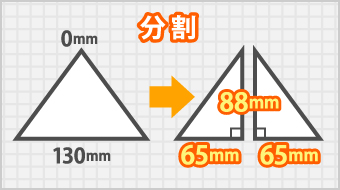
（3）二等辺三角形を頂角と中心として垂直方向の線対称に分割、直角三角形を作る

　上の説明では分かりにくいと思うので、図を見てください。
　これで対辺65mm、隣辺88mm、高さ88mmの直角三角形ができました。

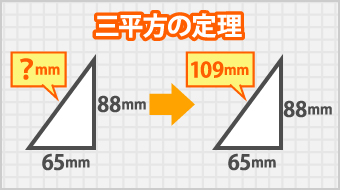
（4）斜辺の長さを計算する

　ここで三平方の定理の出番です。

65の二乗+88の二乗=11969
√11969≒109
　これで斜辺の長さが約109mmだということが分かりました。

（5）　平らな部分を含めた一山（一谷）分の長さを算出する

ヨドルーフ88のこれまで分かっている数値を整理しましょう。

一谷分の長さ

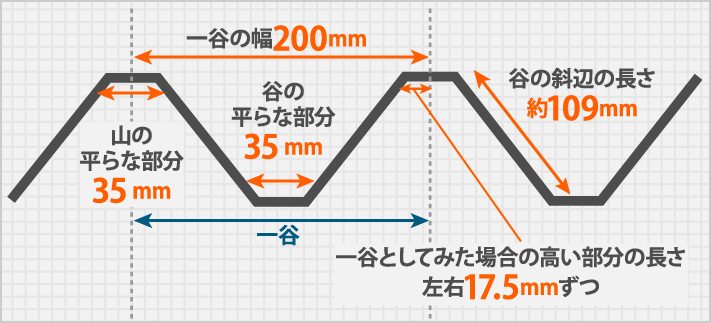
一谷分の長さ=谷の平らな部分35 mm+谷の斜辺の長さ約109mm×2+高い部分の長さ17.5mm×2

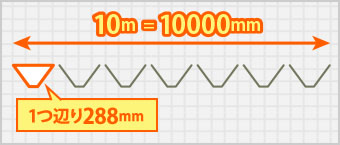
（6）　ヨドルーフ88の横の長さを算出する

　一谷分の長さは288mmとなります。先程の1.4という数値の近似値になりました。これで後は谷（山）の数を数えて、それに凸凹に対して平行の長さをかければ折板屋根の表面積となります。
　谷（山）の数を数えるのが面倒な場合は凸凹に対して垂直の長さを測り、一谷の幅200mmで割れば、谷の数も分かるので面積を求めることが可能です。